Explicamos o que é um polígono em geometria, os elementos que o compõem e que tipos existem. Além disso, como suas medidas são calculadas.

O que é um polígono?
Em geometria, um polígono é chamado de uma figura geométrica plana, composta por um conjunto de segmentos de reta conectados de tal forma que encerram e delimitam uma região do plano, geralmente sem cruzar uma linha com outra. Seu nome vem das palavras gregas poli (“muito e gonos (“ângulo”), ou seja, que em princípio são figuras geométricas com numerosos ângulos, embora hoje em dia se prefira classificá-los segundo o número de lados e não de ângulos.
Polígonos são figuras bidimensionais (equivalentes planos de politopos tridimensionais), ou seja, possuem apenas duas dimensões: comprimento e largura, e ambas são determinadas pelas proporções das linhas que os compõem. O fundamental de um polígono é que o conjunto de suas linhas separa uma região do plano das demais, ou seja, delimita um “dentro” e um “fora”, pois são figuras fechadas em si mesmas.
Existem muitos tipos de polígonos e muitas maneiras de entendê-los, dependendo se estamos falando de geometria euclidiana ou não euclidiana, mas Eles geralmente são nomeados dependendo do número de lados que possuem, usando prefixos numerais.. Por exemplo, um pentágono (penta + gonos) é um polígono que tem cinco lados reconhecíveis.
O resto dos polígonos são nomeados da seguinte forma:
| Número de lados | Nome do polígono |
| 3 | trígono ou triângulo |
| 4 | Tetrágono ou quadrilátero |
| 5 | Pentágono |
| 6 | Hexágono |
| 7 | Heptágono |
| 8 | Octógono ou octogonal |
| 9 | Nonágono o eneágono |
| 10 | Decágono |
| 11 | hendecágono ou undecágono |
| 12 | Dodecágono |
| 13 | tridecágono |
| 14 | Tetradecágono |
| 15 | Pentadecágono |
| 16 | Hexadecágono |
| 17 | heptadecágono |
| 18 | Um octadecágono ou octadecágono |
| 19 | Nonadecágono o eneadecágono |
| 20 | Isodecágono o icoságono |
| 21 | Henicosagon |
| 22 | Doicoságono |
| 23 | triaicosgon |
| 24 | Tetraicosagono |
| 25 | Pentaicoságono |
| 30 | Triacontágono |
| 40 | Tetracontagon |
| 50 | Pentacontágono |
| 60 | Hexacontaagono |
| 70 | Heptacontágono |
| 80 | Octocontágono u octacontágono |
| 90 | Nonacontágono o eneacontágono |
| 100 | hectágono |
| 1.000 | Quiliágono ou Kiliágono |
| 10.000 | Miriagono |
Veja também: Poliedros
elementos de um polígono
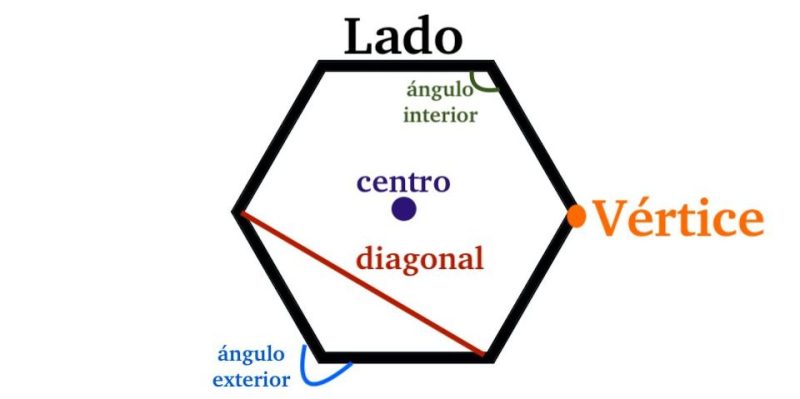
Os polígonos são compostos por uma série de elementos geométricos a ter em conta:
- Lados. São os segmentos de reta que compõem o polígono, ou seja, as retas que o traçam no plano.
- Vértices. São os pontos de encontro, interseção ou união dos lados do polígono.
- Diagonais. São linhas retas que unem dois vértices não consecutivos dentro do polígono.
- Centro. Presente apenas em polígonos regulares, é um ponto de sua área interna equidistante de todos os seus vértices e lados.
- ângulos internos. São os ângulos que compõem na zona interior do polígono dois dos seus lados ou segmentos.
- ângulos externos. São os ângulos que compõem na área externa do polígono um de seus lados ou segmentos e a projeção ou continuação de outro.
tipos de polígonos
Os polígonos são classificados de diferentes maneiras, de acordo com sua forma determinada. Em primeiro lugar, é importante distinguir entre polígonos regulares e irregulares:
polígonos regulares. São aqueles cujos lados e ângulos internos têm a mesma medida, sendo iguais entre si. São figuras simétricas, como o triângulo equilátero ou o quadrado. Além disso, polígonos regulares são ao mesmo tempo:
- Polígonos equiláteros. São aqueles polígonos cujos lados sempre medem o mesmo.
- Polígonos equiangulares. São aqueles polígonos cujos ângulos internos medem sempre o mesmo.
Polígonos irregulares. São aqueles cujos lados e ângulos internos não são iguais entre si, pois possuem medidas diferentes. Por exemplo, um triângulo escaleno.
Por outro lado, os polígonos podem ser simples ou complexos, dependendo se seus lados se cruzam ou secam em algum ponto:
- Polígonos simples. São aqueles cujas linhas ou lados nunca se cruzam ou secam e, portanto, têm um único contorno.
- Polígonos complexos. São aquelas que apresentam um cruzamento ou interseção entre duas ou mais de suas arestas ou lados não consecutivos.
Finalmente, podemos distinguir entre polígonos convexos e côncavos, dependendo da orientação geral de sua forma:
- Polígonos convexos. São aqueles polígonos simples cujos ângulos internos nunca ultrapassam 180° de abertura. Eles são caracterizados pelo fato de que qualquer lado pode estar contido na figura.
- Polígonos côncavos. São aqueles polígonos complexos cujos ângulos internos ultrapassam 180° de abertura. Eles são caracterizados porque uma linha reta é capaz de cortar o polígono em mais de dois pontos diferentes.
medidas de um polígono
Sendo uma figura plana, que existe apenas no plano bidimensional (isto é, comprimento e largura), mas fechada sobre si mesma, os polígonos contêm um segmento do plano e delimitam um exterior e um interior. Graças a isso, dois tipos de medições podem ser feitos:
O perímetro. É a soma do comprimento de todos os lados do polígono e, no caso de polígonos regulares, é calculado multiplicando-se o comprimento de seus lados pelo número destes.
A área. É a porção do plano delimitada pelos lados do polígono, ou seja, sua área “interior”. Seu cálculo, no entanto, requer procedimentos diferentes, por exemplo:
- Em um triângulo, é calculado multiplicando a base e a altura e dividindo por 2.
- Em um quadrilátero regular (quadrado), é calculado elevando ao quadrado o comprimento de qualquer um de seus lados.
- Em um quadrilátero reto (retângulo), é calculado multiplicando sua base por sua altura.
Que figuras planas não são polígonos?
Nem todas as figuras planas são polígonos. Essas figuras que não se fecham sobre si mesmas (ou seja, não possuem área interna), que possuem linhas curvas em sua formação ou cujos lados não consecutivos se cruzam não devem ser considerados como polígonos.
Continuar com: Plano cartesiano
Referências
- “Polígono” na Wikipédia.
- “Etimologia de Polígono” no Dicionário Etimológico Espanhol Online.
- “O que são polígonos?” na Junta de Andaluzia (Espanha).
- “Polygons” (vídeo) no Smile and Learn.
- “Polígono (matemática)” na Enciclopédia Britânica.
